Machine Learning Project
unsupervised learning and reinforcement learning
Unsupervised Learning
Unsupervised learning is one category of techniques in machine learning that aims to find patterns of a dataset without explicit labeling required by supervised learning. Two main methods fall under unsupervised learning are clustering and dimensionality reduction.
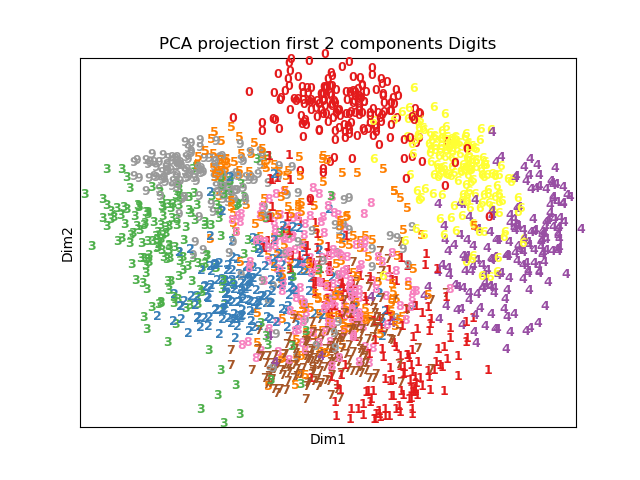
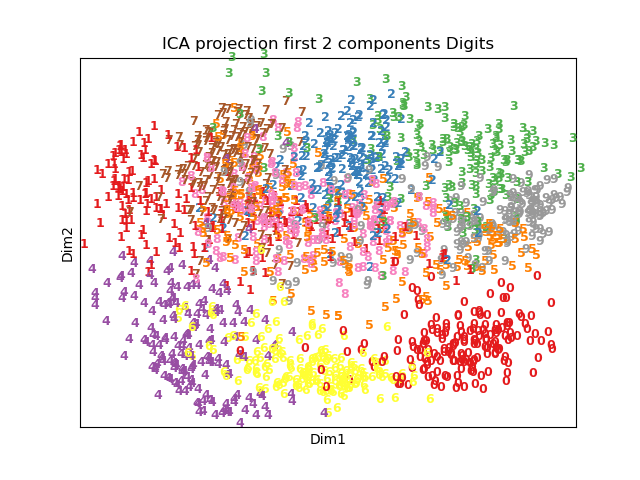
Dimensionality reduction is the method to find more important features and exclude features that are not important. With more features, the data can be sparse and for some models they can suffer from dimensionality curse. In this project, we use primary component analysis (PCA), independent component analysis (ICA) and locally linear embedding (LLE) to conduct dimensionality reduction for MNIST dataset.

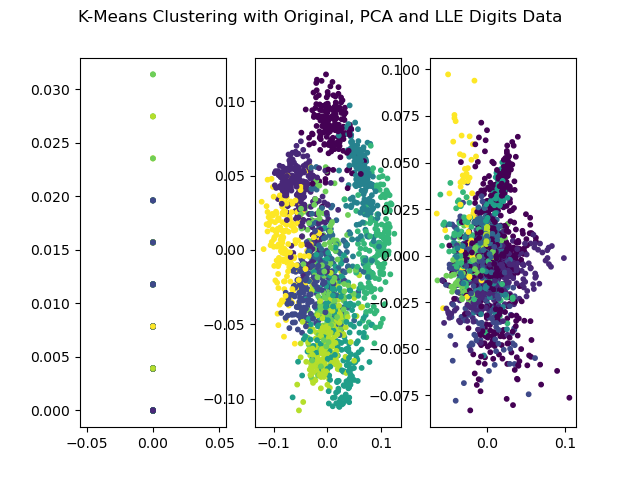
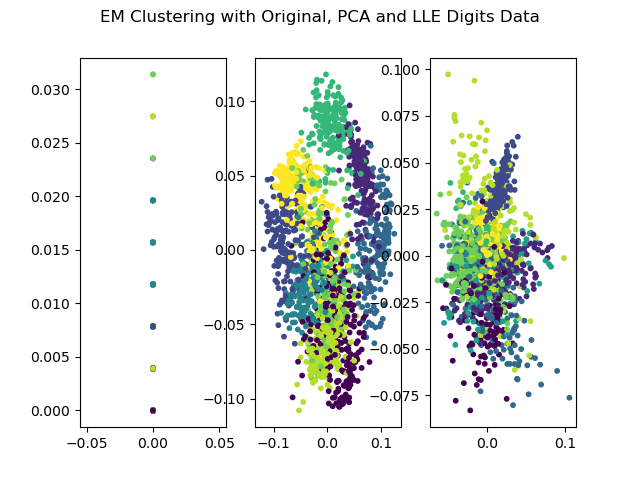
Another method dominates unsupervised learning is clustering, which is to find hidden pattern in a given dataset. Two popular clustering methods are k-Means and expectation maximization (EM). In this project, I show clustering with original dataset and dimensionality reduced dataset.
- Dimensionality Reduction:
- The linearity of the dataset plays a crucial role in the performance of dimensionality reduction methods.
- The chosen dataset exhibits a significant linear relationship, which may explain why the manifold approach, such as LLE, does not perform as well.
- Clustering Using Dimensionality-Reduced Data:
- PCA and manifold LLE were applied for dimensionality reduction, and PCA yielded the best clustering results for the datasets.
Reinforcement Learning
Reinforcement learning is a type of machine learning paradigm where an agent learns to make decisions by interacting with an environment. The agent takes actions, receives feedback in the form of rewards, and learns to maximize its cumulative reward over time.Reinforcement Learning algorithms, such as Q-learning, policy iteration and value iteration methods, use the MDP framework to model the environment and learn an optimal policy. These algorithms aim to find a strategy (policy) that guides the agent to take actions that lead to the highest expected long-term reward.
Policy iteration and value iteration are reinforcement learning methods developed from Bellman equation, which fully encodes the utility of a state in a markov decision process (MDP).
\[U\left(s\right) = R\left(s\right) + \gamma \max_{a\in A\left(s\right)}\sum_{s'} T\left(s,a,s'\right)U\left(s'\right)\]Frozen Lake Problem
%20Gamma%200.99.png)
%20Gamma%200.99.png)
%20Epsilon%200.1.png)
Blackjack Problem
%20Gamma%200.99.png)
%20Gamma%200.99.png)
%20Epsilon%200.1.png)
- Policy Iteration and Value Iteration
- PI and VI would reach to the same optimal policy when they are long-term planning enough to reach the goal.
- PI and VI may show observable difference if the discount rate Gamma is small and they are favoring immediate rewards in different ways.
- When changing Gamma, typically time cost for each iteration in PI would be similar if it is deterministic process, and can change drastically if it is stochastic process.
- When changing Gamma, typically time cost for each iteration in VI would be less sensitive no matter it is stochastic or non-stochastic process.
- PI/VI may not be very robust when solving stochastic problem like Blackjack.
- Q Learning
- QL would generate very different optimal strategy compared to PI/VI because of the nature of action selection.
- QL can be more robust when solving stochastic problems like Blackjack.
- In complex problem like with large state space, QL convergence behavior can be very sensitive when tuning epsilon.